Power Analysis by Data Simulation in R - Part I
Part I - theoretical introduction to data-simulation
Power Analysis by Data Simulation in R - Part I: Theoretical introduction to simulation
Why this blog?
In recent years, power-analysis has become a standard tool in the behavioral sciences. With an ongoing replication crisis, high-power research is the a key to improving replicability and to improving the reliability of findings. Especially with preregistration slowly becoming standard practice in psychology, power-analysis, the practice of estimating the required sample-size a-priori, is a more important step than ever to plan research projects accordingly.
Not so long ago, power-analysis was a rather complicated endeavor urging people to use algebraic solutions to calculate power of planned studies which can be demanding especially for non-trivial designs (i.e. basically anything that is not a correlation). Luckily, for many research designs power-analysis is nowadays readily available in software packages such as G*Power and even for relatively complex designs in specialized tools such as the great PANGEA tool for all kinds of generalized ANOVA designs and other tools by Jake Westfall.
However, while these tools are really great they also have (in my personal opinion) two drawbacks. First, they urge the user to familiarize themselves with a new piece of software with new user interfaces, that are not always intuitive. Second, and more importantly, these interfaces promote a statistical way of thinking that often leaves the user confused with what the ever-changing parameters (think of these \(\delta\) , \(d\), \(f\), \(f^2\) and vague “group-size” and “measurement-point” fields) that need to be filled in mean. Moreover, these parameters differ for most designs and give an impression that power-analysis is complicated business better left to statisticians or that it might not be worth the effort.

However, this impression changed dramatically for me, once I changed my ways and started doing power analysis by simulation. Moreover, learning how to simulate data can of course not only be of use for power analysis but is a useful skill to in every research project. When we simulate data, we can see whether what we think about the data-generating process will actually result in the patterns that we would expect. In other words, we can do theoretical experiments to see whether if everything goes as we would expect, we would also find the results that we would expect. Especially when our analyses become more complex, all the different parts in our model tend to interact and it is easy to get lost. By simulating data before conducting an experiment, we will be forced (and able) to specify more precisely how we think a theoretical model or prediction will be reflected in the data.
Thus, even though this tutorial will focus on simulating data for power analysis, you will learn a very useful skill on the side - simulating your own data and thereby conducting theoretical experiments before you even collect data.
I know that there are already some excellent tutorials on data/power-simulation out there but they are often very brief and/or technical and assume a rather high level of prior knowledge about R and data-simulation in general.
Therefore, I will spend some time on explaining theoretical concepts and slowly build up the simulation-code to hopefully enable the reader to understand the underlying principles and flexibly conduct power simulations themselves after reading this.
Throughout the tutorial I assume readers are familiar with R and some of it’s base functionality.
This tutorial will consist of four different parts.
- In the first part (the one you are reading) I will give a short overview of how power-analysis by simulation works on a conceptual level and why I prefer it to available power-analysis software, even though there are clear drawbacks that I will also briefly mention. Moreover, I will introduce the concept of power as I want to bring us all on the same page and want to give a (hopefully) intuitive example about what we actually do in power calculation and how it relates to the simulation techniques that we will use for the rest of the tutorial.
- In the second part, I will discuss simulations for the simplest case of paired and two-sample t-tests.
- In the third part, we will explore different ANOVA and regression designs.
- In the fourth part we will move on to more complex mixed-effects and hierarchical models and even have a peak at Bayesian approaches to power analysis (well technically its not a power analysis but a true detection rate analysis).
For this fourth part, I assume readers will be familiar with how to fit mixed-effect models in
lmerand/orbrms.
This part of the tutorial is by far the most wordy and longest part. Just as a little motivator to keep in mind during this sometimes lengthy tutorial: At the end of part IV of this tutorial, you will know how to do your own custom power analysis for mixed-effects models.
Power Analysis by Simulation (a sustainable alternative)

What is power again? A brief introduction
As my intention is to keep this post as short as possible (SPOILER: which definitely did not work), let’s directly dive into the topic by having a look at the definition of power:
If a certain effect of interest exists (e.g. a difference between two groups) power is the chance that we actually find the effect in a given study.
To provide some intuition about power, lets assume you toss a coin 10 times and you get 10 heads. Should you be surprised about this? Intuitively, it makes sense that we should be more surprised the more often we toss the coin and it keeps landing on head. 10 out of 10 heads would for example be less surprising than 10,000 out of 10,000, right? This is exactly the question we want to answer when with power analysis1. How often should we toss the coin until we are surprised enough to conclude that the coin is not fair.
To translate the above situation into a Frequentist null-hypothesis significance testing (NHST) scenario, we hypothesize that the coin is indeed fair (null-hypothesis) and see whether or not the observed number of heads (the observed data) fits with this hypothesis or not. If yes, we will retain the null-hypothesis that the coin is fair, if not, we will conclude that the data are very unlikely to result from tossing a fair coin.
How do we do this? Well, assume we observed 3 heads out of 3 total tosses. Now we can count all ways that this could have happened with a fair coin and compare it to all possible outcomes that our coin toss experiment might have produced. These possibilities are (for a fair coin or any coin that cannot produce only heads or only tails):
| Toss #1 | Toss #2 | Toss #3 | number of heads | |
|---|---|---|---|---|
| Possibility #1 | HEAD | HEAD | HEAD | 3 |
| Possibility #2 | HEAD | HEAD | TAIL | 2 |
| Possibility #3 | HEAD | TAIL | TAIL | 1 |
| Possibility #4 | TAIL | TAIL | TAIL | 0 |
| Possibility #5 | TAIL | TAIL | HEAD | 1 |
| Possibility #6 | TAIL | HEAD | HEAD | 2 |
| Possibility #7 | TAIL | HEAD | TAIL | 1 |
| Possibility #8 | HEAD | TAIL | HEAD | 2 |
Notice that a possibility is not only defined by the number of heads and tails but also by the order in which they occur2. We can also calculate the number of possibilities as \(2^x\) where 2 means that we have 2 possible outcomes per toss and \(x\) is the number of tosses. In this case the number of possibilities is therefore \(2^3 = 8\). Only 1 of these 8 events (Possibility 1) can produce 3 out of 3 heads. If our coin is fair, each of these events should be equally likely and we can see that when flipping a fair coin 3 times, in only 1 out of 8 cases (12.5%) we will get 3 heads (Possibility 1).
Do we find this surprising enough to conclude that the coin that we flipped is unfair? Maybe, maybe not. If not, instead of flipping the coin three times, we could flip it 100 times. Imagine we observed 55 heads in 100 flips. We could now start writing down all possible outcomes, but that would take some time. This time, there are not 8 but \(2^{100}\) = 1,267,651,000,000,000,000,000,000,000,000 possible sequences of heads and tails, and we would have to count the ones that produce at least 55 heads to see how often that would happen if our coin is fair3.
However, luckily we are not the first who are interested in these kind of problems and we can make use of mathematical formulas that other people figured out for us.
In this case we need the binomial probability mass function.
In short, this function defines how often we can get each outcome, assuming a certain chance of getting heads or tails.
If you are interested in seeing this function and see how we can hand-code it in R, then click on the info-box below.
If you do not want to get too much into the technicalities here, you can also just read on.
Click here to extend information about the binomial likelihood function
Click here to extend information about the binomial likelihood function
\[P(x)=\frac{N!}{x!(N-x)!}\pi^x(1-\pi)^{N-x} \]
For people who are not used to mathematical formulas, this might already look intimidating. However, all we need to know right now is that this formula gives us the probability of getting x heads \(P{(x)}\) (i.e. the number of ways we get x heads divided by N tosses): Note that \(\pi\) in the above formula is not the one we might know from geometry but it is simply the Greek letter for p denoting a probability here. In this case, it is the probability of either event, heads or tails, happening on each toss so it is 50% or 0.5. We can fill this in for the example above:
\[P(55)=\frac{100!}{55!(100-55)!}0.5^{55}(1-0.5)^{100-55}\]
Translating this formula into R syntax we get the following:
factorial(100)/(factorial(55)*factorial(100-55))*0.5^55*(1-0.5)^(100-55) = 0.05
However, before we said that we do not need the probability of exactly 55 heads but everything that is at least 55. In order to answer our question how often we get at least 55 heads, we could repeat the above calculation with all values from 55 up until 100 and add up the probabilities that we get.
For example we could do this with a for-loop:
# first we write a function that calculates the probability for each number so we can call it in a loop
pbinom2 <- function(N, x, p){
factorial(N)/(factorial(x)*factorial(N-x))*p^x*(1-p)^(N-x)
}
tosses_55to100 <- c(55:100) # we define the amount of heads that we want to check for (all bigger than or equal to 55)
probs <- c() # we will make an empty collection that we will add the results for each number of heads to
for(i in tosses_55to100){
probs <- append(probs, pbinom2(100,i,.5))
}
print(probs[1:10])## [1] 0.048474297 0.038952560 0.030068643 0.022292270 0.015869073 0.010843867
## [7] 0.007110732 0.004472880 0.002697928 0.001559739Now we got all the probabilities for each of the amounts of heads that we are interested in.
By summing them up we get what we need - the probability of getting at least 55 heads in 100 tosses, sum(probs) = 0.18 or 18 percent.
As mentioned, fortunately, the counting of possibilities is pre-implemented into R.
Running pbinom(x = 54, size = 100, prob = .5, lower.tail = FALSE) (I will explain below) we can get R to calculate the proportion of samples that would result in more than x times heads in an experiment of size 100 (i.e. tossing a coin 100 times).
Executing this in R we get 0.18.
In short, the pbinom function gives us the answer to the question "what is proportion of possible toss-sequences that results in more than x = 544 heads if we toss a coin size=100 times if our hypothesis is that the coin is fair with a probability of heads of prob = .5.
The lower.tail = FALSE argument tells R that we want the the probability of the upper part of the probability mass (i.e. the probability of getting 55 or more heads rather than 54 or less).
In other words, every 6th out of the \(2^{100}\) possible sequences has 55 or more heads.
Again, this is not really surprising and would probably not make us conclude that a coin is definitely unfair.
If, for example, we think that a coin is unfair if the amount of heads (or more heads) has only a probability of .01 or 1 percent, what amount of heads would allow us to draw such a conclusion when tossing a coin 100 times?
To solve this, we can just use the pbinom function for not only x = 55 heads but also 56 up to 100 heads, and see from which point onwards only 1 percent of all \(2^{100}\) sequences include so many heads.
The code below does exactly this.
Conveniently the pbinom function cannot only evaluate 1 value at the same time but we can just pass all values that we want to try as a sequence and it will give us the probability of x heads for each of them so we can store them as a collection of values.
We can plot these values to see when we cross the 1 percent line.
n_heads <- 54:99 # all possible amount of heads that we want to try.
p_heads <- pbinom(q = n_heads, size = 100, prob = .5, lower.tail = F) # get pbinom to show us the probability of so many heads for each of the values if a coin is fair
plot(n_heads, p_heads)
abline(h = .01)
abline(v = n_heads[p_heads < .01][1])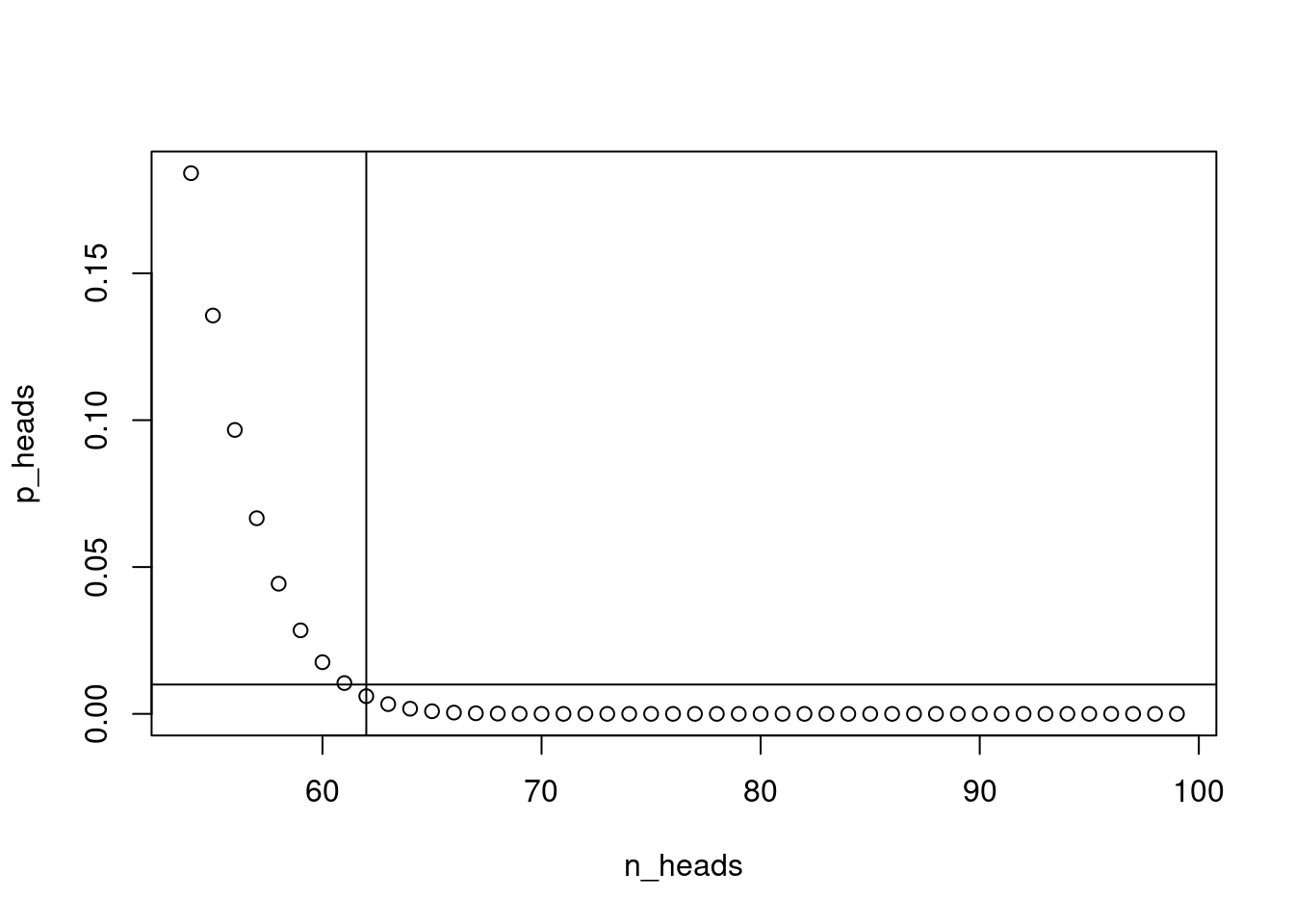
Using the above we see that the at n_heads[p_heads < .01][1] = 62 tosses, i.e. the 9th element of the vector is the first probability that is smaller than .01, in this case 0.006.
In other words, getting 62 or more heads in 100 tosses would only happen extremely rarely, in 1 out of 62 cases.
Thus actually getting 62 heads is pretty surprising and if something like that happened we might conclude that a coin is unfair.
However, instead of following the approach above, there is an easier way to get the number of heads that would surprise us by using the qbinom function that gives us the quantile (i.e. number of heads or more heads) that would only happen with a certain probability: qbinom(p = .01, size = 100, prob = .5, lower.tail = FALSE) = 62, unsurprisingly gives us the same result.
Back to Power
In this coin-toss example, we run a statistical test about the fairness of the coin. But what is the power of the test here (in case you forgot during my very long “brief” introduction, this post was about power)?
Actually, we already used three concepts from Frequentist statistical testing:
- The null-hypothesis: we assumed that the coin is fair
- The p-value : the probability that we calculated above when checking how likely 62 or more heads are (we got 0.006).
- The alpha level : (i.e. where people conventionally use .05 in psychological literature5) is the threshold that we picked for concluding it would surprise us enough to say that the coin must be unfair, i.e. the probability of .01. In other words, it is the chance that we conclude that a coin is unfair even if it is actually fair (the one percent of cases where 62 or more heads would happen even with a fair coin).
In a proper power analysis, all of these need to be specified in addition to an alternative hypothesis. Let’s give it a try and specify them to run a power-analysis
Specifying the null-hypothesis.
Again, we will assume that a coin is fair and will produce heads with a probability of .506.
Specifying the Alternative Hypothesis aka Effect Size.
To conduct a proper power-analysis, it is important that we specify a concrete alternative hypothesis (or effect size). If we do know have a hypothesis about the effect size, we can by definition not know the power to investigate this hypothesis. Makes sense, right?
This means we will try to think about an effect size that would be meaningful in this coin flip example. For instance, if you use the coin to make an important decision, i.e. when the fairness of the coin is very important (see e.g. Figure 3)7 you would probably want to be very strict about when a coin is unfair and would like to, for instance, already conclude that it is unfair at 55% percent heads, a deviation from a truly fair coin of 5%.
Most software packages use effect-size estimates like Cohen’s d or f or other standardized effect sizes. We will have a look at how to do this with simulations briefly in the second part of the tutorial, but throughout this tutorial, we will mostly follow a different approach by trying to specify the expected effect size on the raw scale.
Specifying the alpha-level
Furthermore, as it does not deem you a good idea to get into a fight with Harvey (Figure 3) by incorrectly accusing him of using an unfair coin, you want the chance of this happening (i.e. the alpha-level) to be very low at only 0.1 percent (1 in a 1000 cases)9.
Specifying the desired power
Moreover, you also want to be sure that you would detect the unfairness of 55% if it is actually there. Let’s say you only want to have a 10 percent chance of not detecting it if it was there. 100 minus this chance is the power of our coin-toss study, i.e. 90 percent (or 1-.10 on the probability scale).

To summarize, our test has the following properties:
- alpha-level = .001
- alternative hypothesis (aka effect size / fairness-criterion) = 55% heads
- power = .90
Our job now is to figure out at which number of tosses we can be 90% sure to detect the unfairness of 55% with only a 0.1% chance of getting into a fight with Harvey by wrongly accusing him of unfairness.
To do this we can use the following r-code (I will explain below)
The first Power Calculation
power_at_n <- c(0) # initialize vector that stores power for each number of tosses
n_heads <- c() # save "critical" number of heads for that toss-amount that would result
n_toss <- 2 # initialize the toss-counter
while(power_at_n[n_toss-1] < .90){ # continue as long as power is not 90%
n_heads[n_toss] <- qbinom(.001, n_toss, .5, lower.tail = F) # retrieve critical value
power_at_n[n_toss] <- pbinom(n_heads[n_toss], n_toss, .55, lower.tail = F) # calculate power (1-beta) for each coin-toss
n_toss <- n_toss+1 # increase toss-number
}The above loop needs some explanation.
It increases the toss-amount n_toss by 1 as long as it has not yet reached 90% power.
To do this, we again use the qbinom function to find the number of heads (or more heads) that would only occur with a probability of .001.
In other words, only 0.1% of the possible coin toss sequences would result in that specific amount of heads when tossing the coin n_toss times.
This is the same thing we did earlier with a fixed amount of 100 tosses.
in the next line, we take this amount of heads that only occurs with a probabiltiy of .001 for the current toss amount n_toss and use pbinom to calculate the probability of getting at least this many heads with our hypothesized unfair coin that produces heads in 55% of the cases.
This means, we calculate the percentage of coin toss sequences that contain at least this many heads.
This probability is the power of the test.
Why?
Because if 90% of the sequences contain 55% or more heads, if we take the coin and toss it n_toss times,in 90% of the cases we will get one of those sequences that contain 55% or more heads.
Lets have a look at two of the values from this calculation to make this more clear. For instance, lets look at the values when the loop tried out 100 tosses:
n_heads[100] = 65. This number is higher than the 62 heads we had above, as we are more strict now by specifying a stricter alpha level (.001 instead of .01).
Next, this 65 was passed on to the pbinom function and we can look at the power, power_at_n[100] = 0.02.
At this point we only have a power of .02 or 2%.
This means that tossing an unfair coin that would give 55% heads 100 times, only 2% of the sequences would contain 55 or more heads, therfore making it unlikely that we would detect the unfairness.
When we increase the number of tosses until the loop stops, we are at n_toss-1 = 1908 coin tosses.
At this number of tosses, the amount of heads that would make us conclude that a fair coin is unfair (biased with 55% heads) with only 0.1% chance of being wrong is n_heads-[n_toss-1] = 1021.
Thus in this case, with 1908 tosses, if we get 1021 heads or more, we conclude that the coin is unfair.
What is the chance of getting at least that with our unfair coin?
That’s what the pbinom function in the loop above tells us and it is power_at_n[n_toss-1] = 0.9, our specified 90%.
We can also plot the power for each number of tosses that we tried in the loop.
Figure 4 shows the increase in power with increasing sample-size.
plot(1:(n_toss-1), power_at_n, xlab = "Number of coin-tosses", ylab = "Power", axes = FALSE)
abline(h = .90, col = "red")
axis(side = 1, at = seq(0,(n_toss-1),by=100))
axis(side = 2, at = seq(0,1,by=0.1))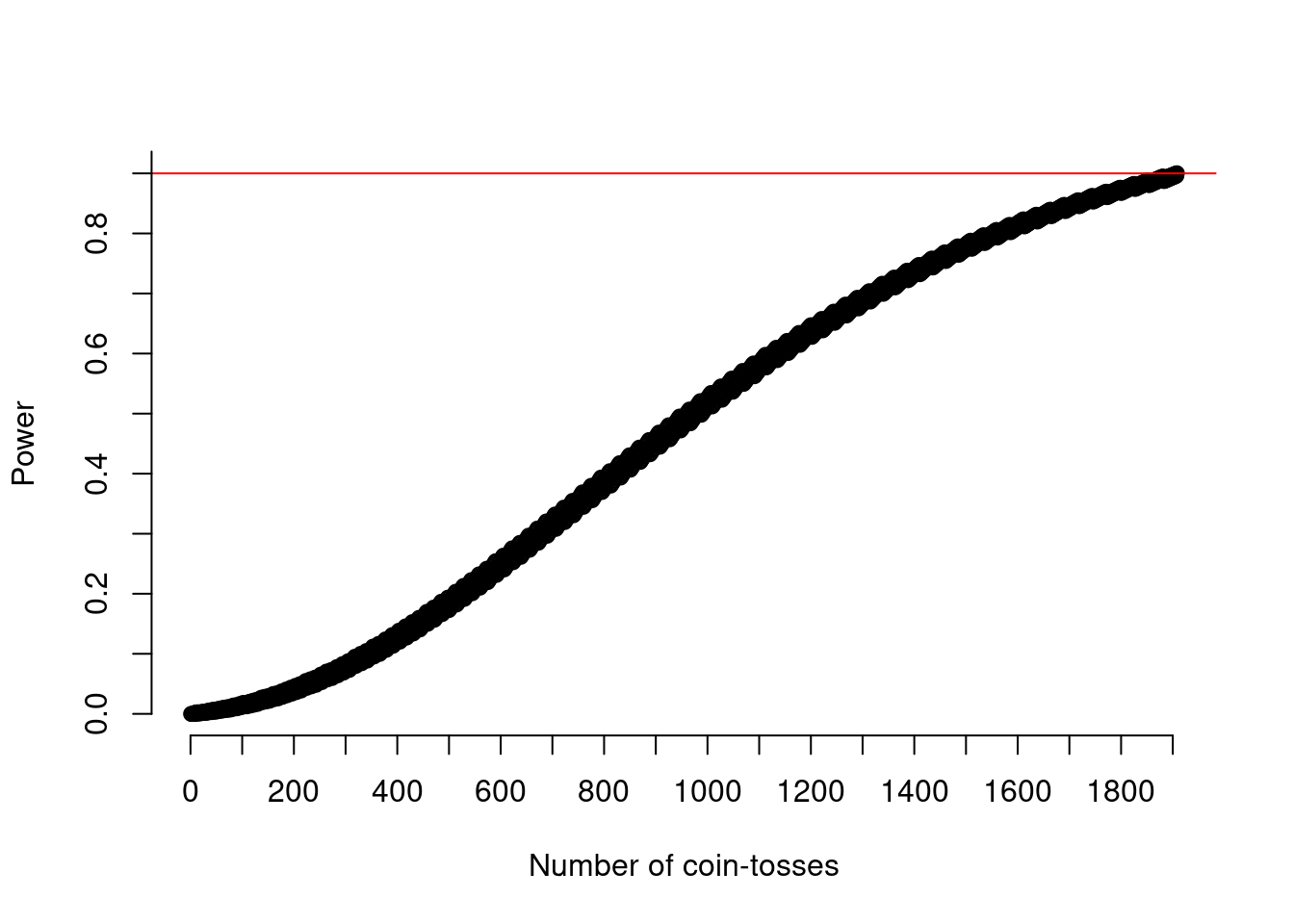
Thus, when tossing a coin 1908 times10, in 90% of the cases we will be able to tell it’s biased and can confidently confront Harvey like shown in Figure 5.

If you are not familiar with using these distribution functions (qbinom, pbinom etc.) in R, this might have been a lot of new information but this is basically what we do in power analysis:
- We specify a null-hypothesis, an alternative hypothesis, an alpha-level and a desired power,
- We try a small sample-size.
- We retrieve the critical value, (the number of heads that would be more surprising than what we specified as our alpha-level).
- We calculate the probability that the amount of heads that would make us reject the null-hypothesis would be observed with the unfair coin according to the alternative hypothesis.
- We stop as soon as this probability is equal to the desired power.
Finally, an actual power simulation.
So far, we have not done any simulation but have merely analytically derived the power by making use of the binomial probability mass function11. Thus, for easy toy-examples like this one we would not need to do a simulation. However, as soon as we deal with real examples, it is much more difficult to make use of this approach and if we have several predictors in our model, or if we deal with mixed-effect models or hierarchical models (as we will do in part IV of this tutorial) the above method is not feasible anymore.
What we can do however, for any model of any complexity and form, is to actually pretend we were repeatedly doing the experiment for each sample size and see how often we would be able to reject the null-hypothesis. For instance we could toss a coin 20 times and test whether we would reject the null-hypothesis. We could then repeat this process for 20 tosses very often, e.g. 1,000 times and see what the probability is that we would conclude that the null-hypothesis is false12. This is what we do in power-simulation.
An obvious disadvantage is that instead of just calculating the power for each toss-amount (i.e. sample-size) only once, we need to try each toss-amount out 1,000 times. Thus, simulation takes much longer than a regular power-calculation, especially with more complex models and high sample-sizes. However, the advantage of the method is that we can just learn it once and adjust it for any situation that we will ever find ourselves in, not having to ever walk through tedious interfaces again, selecting arbitrary analyses and setting ever changing parameters to certain values. Another advantage (that will be discussed in detail later) is that we do not need to specify a precise alternative hypothesis and test it for that single value, but that we can actually remain more vague about what our alternative hypothesis (i.e. the effect size that we expect) will be. Oftentimes we do not know exactly what effect-size we can expect and we might like to tell the power-analysis about this uncertainty.
At last, let us do a power-simulation for the above example.
Luckily we do not really have to toss a coin as R can do that for us by using the rbinom function, that will as often as we call it do a coin-tossing experiment for us with a specified sample-size.
Lets first see how the rbinom function works if we would want to toss a coin 20 times.
set.seed(1) # make sure our simulation will give the same results if you try it
rbinom(n = 1, size = 20, prob = .50) # let r do 1 experiment with 20 coin tosses of a fair coin## [1] 9In the above code, R tossed a coin 20 times and it resulted in 9 heads.
We could repeat this experiment again:
set.seed(2) # make sure our simulation will give other results than before
rbinom(n = 1, size = 20, prob = .5) # run the experiment again## [1] 8In this case, giving us 8 heads.
By increasing the first argument to the rbinom function, we can tell R to repeat this experiment more often.
Moreover, we can tell it to make use of an unfair coin directly, so we can directly put our alternative hypothesis in the simulation by changing the last number of the rbinom function from .50 to .55, to do the same test as above.
set.seed(1)
n_heads <- rbinom(n = 1000, size = 20, prob = .55) # run 1,000 experiments, of 20 coin tosses each, at once
str(n_heads) # show structure of vector## int [1:1000] 12 12 11 8 13 8 7 10 10 14 ...Now, R repeated the 20 coin-toss experiment 1,000 times with an unfair coin of 55% chance of resulting in heads giving us 1,000 times the amount of heads that it got.
Let us again now test how big our power was in this case, again with an alpha-level of .001.
p_heads <- pbinom(n_heads, 20, .50, lower.tail = F) # calculate the probability of observing this many heads if the coin would be fair (which it is not cause we simulated with 55% heads)
exp_power <- mean(p_heads < .001) # check where this chance drops below our alpha levelThe first line in the above code does exactly what we did earlier, just with a little change.
We take the amounts of heads that we got from an unfair coin, and check in how many cases we would conclude - assuming that the coin would actually be fair, thus using .50 as the probability in pbinom - that the observed amounts of heads is too unlikely for us to believe that the coin was fair.
We save these probabilities to a vector.
The second line calculates the observed power of our experiment.
To understand what it does, let us have a look at the vector p_heads it looks the following (here only the first 10 out of 1,000 values):
p_heads[1:10]## [1] 0.13158798 0.13158798 0.25172234 0.74827766 0.05765915 0.74827766
## [7] 0.86841202 0.41190147 0.41190147 0.02069473As shown above, the p_heads vector contains the probability of observing each amount of heads n_heads from our 1,000 experiments assuming the experiment was done with a fair coin (which it was not).
Now we would like to check how many of these probabilities are at least as small as our alpha-level, i.e. surprising enough to conclude the coin was not fair.
We do this by checking for each value whether it was .001 or smaller (p_heads < .001).
This will result in another vector of 0 when the condition is false and 1 when the condition is true13.
Taking the mean of this vector will give us the probability of rejecting the null-hypothesis while we actually know it is incorrect (as we put the bias in the coin ourselves).
Again, this will give us the power.
In the present case with 20 coin-tosses the power is exp_power = 0.004 or 0.4 percent.
This is obviously very low and not surprising given that we already know from the calculation above that we need a lot more coin-tosses than 20 to get the desired power of 90%.
To get to our desired power in this example, we need to change the code above so it will try different sample-sizes again.
set.seed(1)
exp_power_at_n <- c(0) # create a vector where we can store the power for each sample-size
n_toss_start <- 19 # start at 21 tosses
n_toss_loop <- 2 # additional number of tosses tried (above 20)
while(exp_power_at_n[n_toss_loop-1] < .90){ # continue increasing the sample-size until power = 90%
n_toss <- n_toss_start+n_toss_loop # calculate the current number of tosses
n_heads <- rbinom(1000, n_toss, .55) # run 1000 experiments for any given number of tosses and store number of heads
p_heads <- pbinom(n_heads, n_toss, .50, lower.tail = F) # calculate the probability of getting at least that many heads if the coin would be fair
exp_power_at_n[n_toss_loop] <- mean(p_heads < .001) # calculate power by checking what proportion of the probabilities is smaller than or equal to our alpha-level
n_toss_loop = n_toss_loop+1
}
exp_power_at_n <- exp_power_at_n[-1] # remove the first 0 that we used to populate the vector for the first iteration of the loopThe above code is similar to what we have done earlier when we tried only 1 sample-size.
This time, we iterate over different sample-sizes in a loop and store the power for each in the vector exp_power_at_n.
As in the earlier calculation, we can now use this to see how many tosses we would need by having a look at where the loop stopped, i.e. when it reached 90% power, which is at n_toss-1 = 1795 tosses at which the power was exp_power_at_n[length(exp_power_at_n)] = 0.903.
We can also plot all these values again as done in Figure 6.
plot(21:n_toss, exp_power_at_n, xlab = "Number of coin-tosses", ylab = "Power", ylim = c(0,1), axes = FALSE)
abline(h = .90, col = "red")
axis(side = 1, at = seq(0,(n_toss),by=100))
axis(side = 2, at = seq(0,1,by=0.1))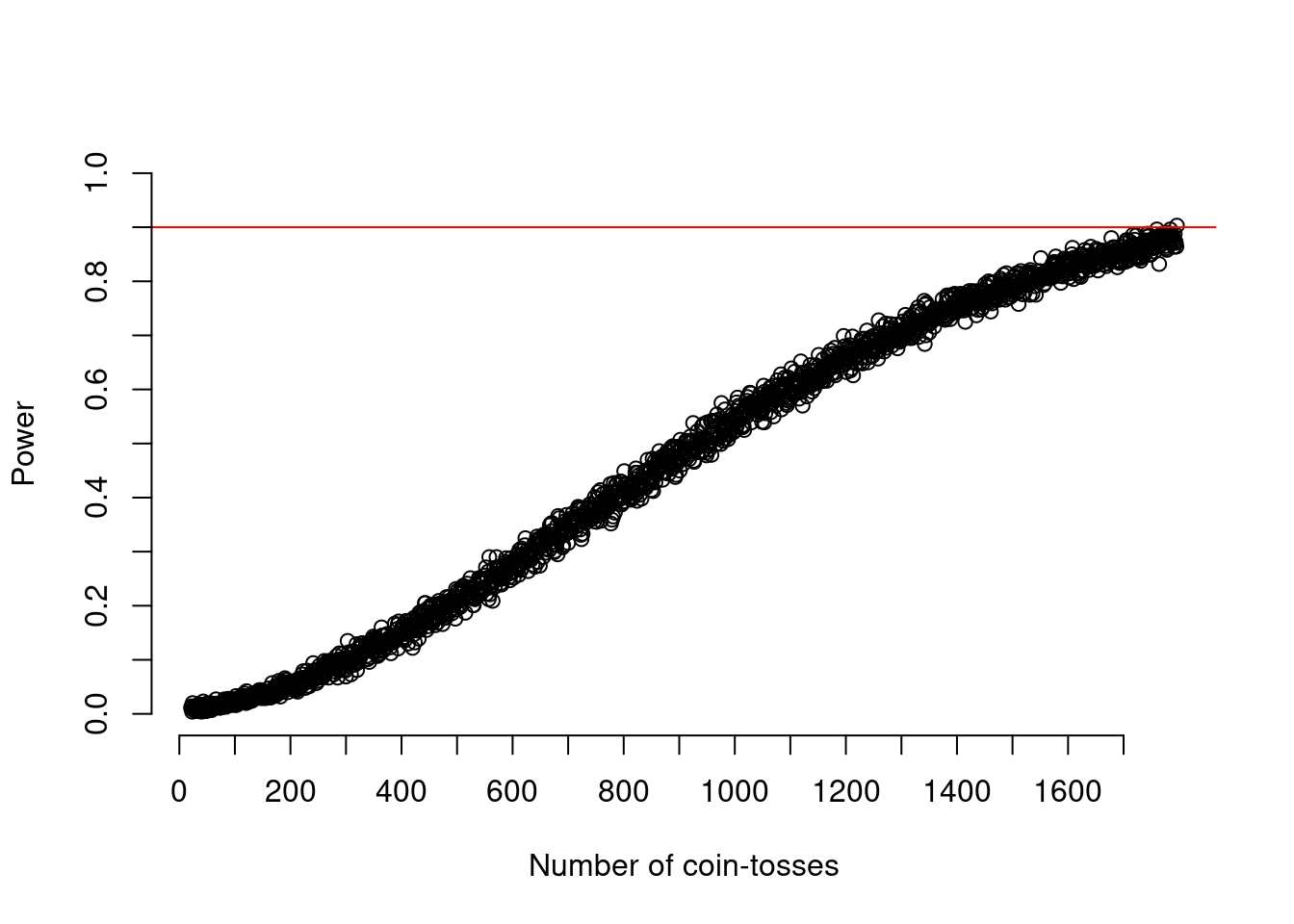
The shape of the line looks very similar to the earlier calculation, however the line appears to be thicker. Moreover, it might be surprising that we did not get the same amount of tosses that we got from the calculation. Actually they differ quite a lot (1908 vs. 1795). This is due to the fact that even when running 1,000 experiments for each sample-size there is still imprecision in the simulation. Each coin-flip is random and even if we repeat a experiment 1,000 times this randomness is still in there (think of how many possible sequences there would be!). This randomness is why we cat a different number in the simulation and why the line in Figure 6 is thicker than in Figure 4.
If we want to approach the results of the calculation more closely in our simulation (i.e. get a more precise power-estimate) we can increase the number of experiments that R will run per sample-size (i.e. the number of simulations).
For example, we could repeat the simulation with 100,000 experiments per sample-size.
You have to be patient here, this already takes a few minutes maybe.
set.seed(1)
exp_power_at_n <- c(0) # create a vector where we can store the power for each sample-size
n_toss_start <- 19 # start at 21 tosses
n_toss_loop <- 2 # additional number of tosses tried (above 20)
while(exp_power_at_n[n_toss_loop-1] < .90){ # continue increasing the sample-size until power = 90%
n_toss <- n_toss_start+n_toss_loop # calculate the current number of tosses
n_heads <- rbinom(100000, n_toss, .55) # run 1000 experiments for any given number of tosses and store number of heads
p_heads <- pbinom(n_heads, n_toss, .50, lower.tail = F) # calculate the probability of getting at least that many heads if the coin would be fair
exp_power_at_n[n_toss_loop] <- mean(p_heads < .001) # calculate power by checking what proportion of the probabilities is smaller than or equal to our alpha-level
n_toss_loop = n_toss_loop+1
}
exp_power_at_n <- exp_power_at_n[-1] # remove the first 0 that we used to populate the vector for the first iteration of the loopIf you run this code, you will see that it took substantially longer than the previous simulation with only 1,000 repetitions.
If we now look at the outcome again we find that the number of tosses n_toss-1 = 1870 is already slightly closer to the calculated value but still not exactly the same.
In my personal opinion, this imprecision is both advantage of simulation as well as disadvantage.
It is a disadvantage in that it is less precise than the calculation above in theory.
However, it is an advantage as it adds some noise to the power-estimation process that is actually also present in real life.
This is, even if there is an effect in the population, each new sample will always be different which is also the case in the simulation.
If we look at Figure 7, we also see that now the power-increase follows a more straight line again that is very close to the one from the exact calculation and not as thick anymore as in Figure 6.
plot(21:n_toss, exp_power_at_n, xlab = "Number of coin-tosses", ylab = "Power", ylim = c(0,1), axes = FALSE)
abline(h = .90, col = "red")
axis(side = 1, at = seq(0,(n_toss),by=100))
axis(side = 2, at = seq(0,1,by=0.1))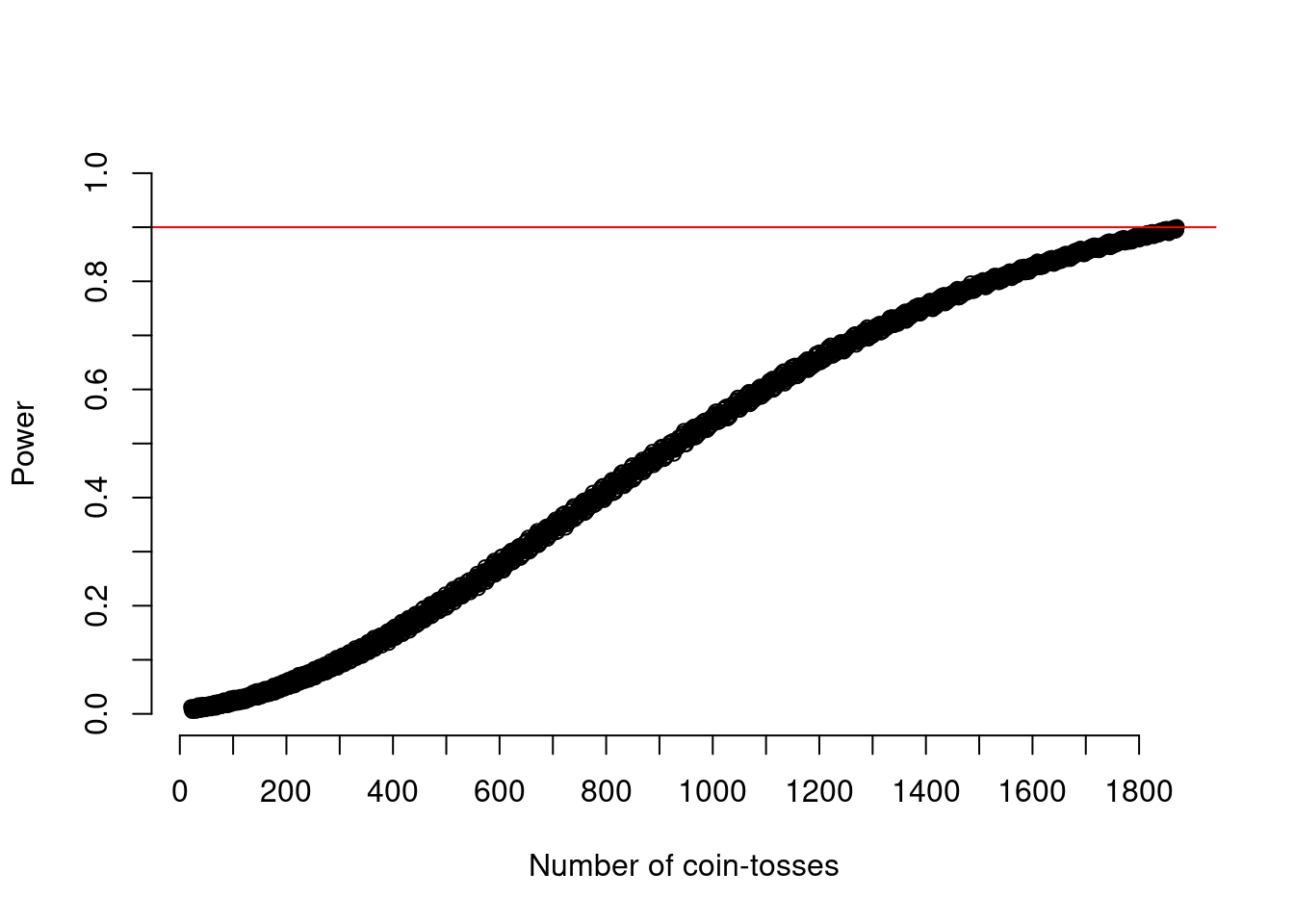
Summary
In this part of the tutorial I tried to bring us all on the same page about why we would do data or power simulation and how it is related to exact power calculation.
- In principle, in power calculation we count the amount of potential data sequences (e.g. possible sequences of HEADS-TAILS in coin-tosses) that could happen in an experiment of a specific size (e.g. amount of coin-tosses).
- Afterwards, we calculate the critical value (e.g. number of heads) that would make us reject the null-hypothesis (e.g. a coin is fair) as only a very small percentage of sequences (“small” is defined by the alpha-level here) would surpass the critical value.
- Finally, we calculate the percentage of sequences according to the alternative hypothesis (e.g. a coin is unfair with a bias of 55%) that would surpass the critical value. This is the power of our test.
In power-simulation we do something very similar, but instead of calculating how many possible data sequences there are and how many of them result in a critical value, we just try this out a lot of times until we get an approximation of how often we would observe data that are inconsistent with the null-hypothesis given our specified alpha-level.
I hope you forgive my rather lengthy introduction on power-analysis before actually doing the simulation, as I thought it would be a good foundation before we move on to more complex and realistic situations.
- In part II of this tutorial, we will move on to these more realistic situations that we might actually be interested in psychology by looking at how we do simulations for t-tests.
- In part III we will continue with ANOVA and regression designs.
- In part IV we will look at mixed-effects/multilevel models.
Footnotes
The answer to the question - Should we be surprised - is basically what we get when we do a statistical test and inspect the p-value. Ok, this is not exactly true but p-values can actually be expressed in terms of how surprised we should be about an observation, given a certain hypothesis (e.g. when we assume no difference between groups as the null-hypothesis). To read an awesome explanation about this, look at this really cool blog-post about s-values by Zad Chow.↩︎
Why is the order important here? Because orders do identify unique outcomes. If we do not consider entire sequences, we might be inclined to think that there are only four possibilities: 3xHEADS, 2xHEADS, 1xHEADS and 0xHEADS, and that each of these events is equally likely. However, how likely each of these events is depends on how many different sequences can produce it.↩︎
I looked it up and apparently this number (a one followed by 30 zeros) is called a Nonillion. It is so big, that apparently the number of bacterial cells on earth is estimated at 5 Nonillion. So I do not recommend trying to write down all possibilities…↩︎
Rexcludes the first number here, so that is why we start at 54 rather than 55↩︎Notice however, that this alpha-level of .05 implies that we are surprised enough if something only happens in 1 out of 20 cases. There have, however, been repeated calls to change the standard alpha-level, to justify it based on the specific situation you are in or to abandon it all together alongside other ideas of using alternatives like the Bayes-Factor. For the most part, in this tutorial I will try to justify the alpha that I choose and to stay away from the “magical” .05 as I agree with the justification approach in that we should at least try and think harder about the alpha-level and it’s meaning.↩︎
It might be confusing that i say “specify” a null-hypothesis here. Is the null-hypothesis not by definition that there is no difference, i.e. that the coin is fair at 50%. Well, yes and no. Of course assuming coin-fairness is the most logical thing to do here but in real life, no matter what research question you are investigating, you will close to always find a difference between groups. If you keep increasing the sample size, at some point the effect will always be significant, no matter how small the deviation is. This is, we could even find the unfairness of the coin if it is only 51%. But is this 51% really big enough to care about? Maybe, maybe not, but we can define a smallest effect size of interest and use Equivalence testing in which the null-hypothesis is a certain range of small deviations from the actual point of no-difference in which we say that the effect is too small to care about. Equivalence testing is not new but surprisingly unknown and/or uncommon in the psychological literature. If you are interested in Equivalence Testing, you should check out the great paper(s) and blog-post(s) about it by Daniel Lakens and colleagues.↩︎
For those unfamiliar with this reference: Consider watching Dark Knight, it’s a great movie. In short, the displayed character, Harvey Dent, a former state lawyer, falls from grace and and loses his faith in the law system. He takes the law into his own hands and decides whether people will be sentenced (i.e. killed) by tossing a coin.↩︎
Software like G*Power often uses different standardized effect sizes for different analyses. However, in many cases standardized effect-sizes can be converted into each other. If you ever need to do such a thing, Hause Lin made a nice conversion app.↩︎
Thereby justifying our alpha-level in this toy example.↩︎
This might be a good point to open G*Power (maybe for the last time ever), to see whether you get the same conclusions there (spoiler: you will, and if not, that only shows that software like this is not necessarily easier to use).↩︎
You can see that is it not a simulation as you will always get the exact same result whenever you run the code above.↩︎
In other words, instead of writing all possible coin-toss sequences down and counting how many of them would produce 55% heads with a certain amount of tosses, we could just run very many experiments in which we for example throw a coin 20 times. If we repeat these 20 tosses 1,000 times, we get an approximation of how many heads the toss sequences produce on average.↩︎
Technically the vector contains FALSE instead of 0 and TRUE instead of 1. However, in R, and many other programming languages, the two are interchangeable, allowing us to calculate the mean in the same way.↩︎